케플러의 행성운동법칙은 독일 천문학자 요하네스 케플러(Johannes Kepler)가 17세기 초에 제시한 세 가지 법칙으로, 행성들이 태양 주위를 도는 운동을 설명합니다. 이 법칙들은 행성의 궤도, 속도, 주기 등을 수학적으로 표현하며, 천문학의 기초 이론 중 하나로 자리잡았습니다. 아래에서는 각 법칙을 수식과 함께 상세하게 설명하겠습니다.
케플러의 행성운동법칙

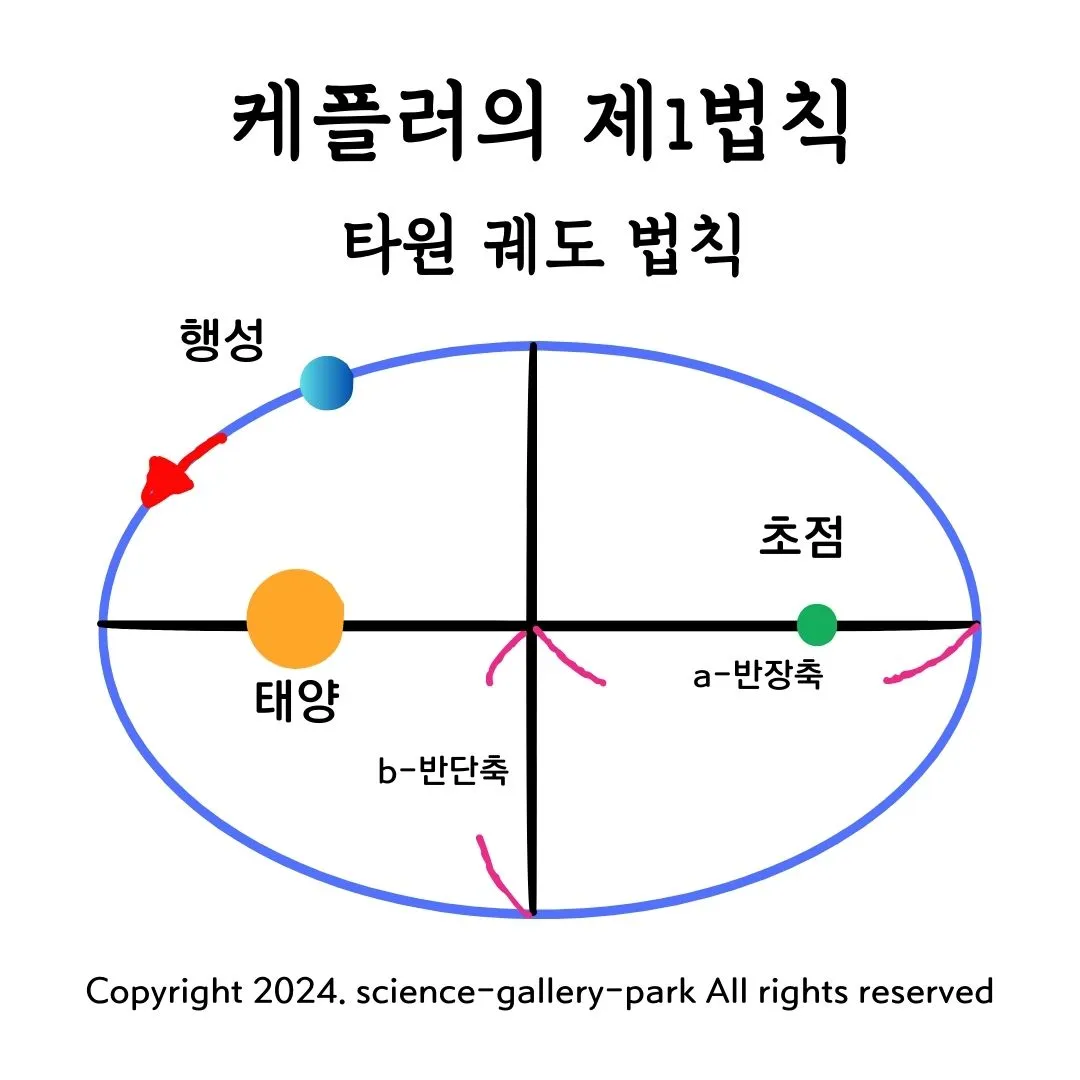
1. 첫 번째 법칙: 타원 궤도 법칙
모든 행성은 태양을 중심으로 한 타원 궤도를 따라 움직인다는 내용입니다. 이 법칙에 따르면, 태양은 타원의 두 초점 중 하나에 위치하며, 행성은 이 타원 궤도를 따라 공전합니다. 이는 당시까지 행성들이 원 궤도를 따라 움직인다고 믿었던 고전적 이론과 달리, 실제 관측 데이터를 기반으로 한 혁신적인 발견이었습니다.
1.1 수식 설명
- 타원은 두 개의 초점을 가지고 있으며, 타원의 임의의 한 점에서 두 초점까지의 거리의 합은 항상 일정합니다.
- 타원의 반장축(semi-major axis) \( a \)와 이심률(eccentricity) \( e \)에 의해 궤도가 결정됩니다.
- 타원의 이심률 \( e \)는 타원의 편평도를 나타내며, \( 0 \leq e < 1 \)의 값을 가집니다.
e = $ \sqrt{1 - \frac{b^2}{a^2}} $
여기서 \( b \)는 타원의 반단축(semi-minor axis)입니다.
1.2 타원 방정식
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $
이 방정식은 타원의 중심이 원점에 있을 때의 방정식으로, 행성의 궤도를 수학적으로 표현합니다.
2. 두 번째 법칙: 면적 속도 법칙
행성이 태양 주위를 공전할 때, 태양과 행성을 연결하는 선이 같은 시간 동안 같은 면적을 휩쓴다는 내용입니다. 이는 행성이 태양에 가까워질수록 더 빠르게 움직이고, 태양에서 멀어질수록 느리게 움직인다는 것을 의미합니다. 이 법칙은 행성의 속도 변화를 설명하는 중요한 원리입니다.

2.1 수식 설명
- 행성의 각운동량 보 법칙에 따라 면적 속도 ( $\frac{dA}{dt} \ $)는 일정합니다.
- 행성의 궤도를 따라 공전하는 동안, 면적 속도는 다음과 같이 표현됩니다:
$ \frac{dA}{dt} = \frac{1}{2} r^2 \frac{d\theta}{dt} = 일정 $
여기서 \( r \)은 태양에서 행성까지의 거리, \( \theta \)는 행성의 궤도 위치에 대한 각도입니다.
2.2 면적 속도 일정
- 면적 속도가 일정하다는 것은 행성이 태양에 가까워질수록(즉, \( r \)이 작아질수록) 각속도 ($ \frac{d\theta}{dt} \ $)가 증가한다는 것을 의미합니다.
3. 세 번째 법칙: 조화의 법칙
행성의 공전 주기와 궤도 반장축의 길이 사이의 관계를 설명합니다. 이 법칙에 따르면, 행성의 공전 주기의 제곱은 궤도 반장축의 세제곱에 비례합니다. 이 법칙은 행성들의 공전 주기와 궤도 크기 간의 조화를 수학적으로 표현한 것으로, 태양계 행성들의 운동을 이해하는 데 중요한 역할을 합니다.

3.1 수식 설명
- 케플러의 세 번째 법칙은 다음과 같은 수식으로 표현됩니다:
$ T^2 \propto a^3 $
이 비례식을 정확하게 나타내면:
$ \frac{T^2}{a^3} = \frac{4\pi^2}{GM} $
여기서,
- \( T \)는 행성의 공전 주기,
- \( a \)는 궤도의 반장축 길이,
- \( G \)는 중력 상수(약 \( 6.674 \times 10^{-11} \, \text{m}^3\text{kg}^{-1}\text{s}^{-2} \)),
- \( M \)은 태양의 질량입니다.
응용:
- 이 법칙을 통해 행성의 공전 주기와 궤도 크기 간의 관계를 수학적으로 계산할 수 있습니다.
- 예를 들어, 지구와 화성의 궤도를 비교할 때, 화성의 궤도 반장축이 지구의 1.524배라면, 공전 주기는 지구의 약 \( \sqrt{1.524^3} \)배가 됩니다.
결론
케플러의 세 가지 행성운동법칙은 천문학과 물리학의 발전에 중대한 영향을 미쳤습니다. 이 법칙들은 태양계의 구조와 행성들의 움직임을 정확하게 설명하며, 뉴턴의 만유인력 법칙의 기초가 되었습니다.
첫 번째 법칙(타원 궤도의 법칙)은 행성들이 완벽한 원이 아닌 타원 궤도를 따라 움직인다는 것을 밝혀, 당시의 천문학적 관념을 뒤집었습니다.
두 번째 법칙(면적 속도 일정의 법칙)은 행성의 공전 속도가 일정하지 않고 태양과의 거리에 따라 변한다는 것을 설명하여, 행성 운동의 역학적 특성을 이해하는 데 큰 도움을 주었습니다.
세 번째 법칙(조화의 법칙)은 행성의 공전 주기와 태양으로부터의 평균 거리 사이의 관계를 수학적으로 정립하여, 태양계의 구조를 정량적으로 이해할 수 있게 해주었습니다.
이 세 가지 법칙은 현대 천문학과 우주 과학의 근간이 되었으며, 우리가 우주를 이해하고 탐험하는 데 필수적인 도구가 되었습니다. 케플러의 업적은 과학적 방법론의 중요성을 보여주는 좋은 예시이며, 관측 데이터의 정확한 분석과 수학적 모델링의 힘을 입증합니다.
결론적으로, 케플러의 행성운동법칙은 우리의 우주관을 혁명적으로 변화시켰으며, 현대 과학의 발전에 지대한 공헌을 했습니다. 이 법칙들은 오늘날에도 여전히 유효하며, 우리가 태양계와 그 너머의 우주를 탐구하는 데 핵심적인 역할을 하고 있습니다.






 }
}