용수철 진자는 물리에서 단진동을 이해하기 위한 대표적인 시스템입니다. 단진동(Simple Harmonic Motion, SHM)은 변위, 속도, 가속도가 서로 주기적으로 변화하며, 이를 통해 에너지의 전환과 동역학의 기초를 배우게 됩니다. 이번 포스팅에서는 용수철 진자의 원리와 가속도와 변위 사이의 관계를 알아보겠습니다.
단진동

1. 단진동(Simple Harmonic Motion)이란?
• 정의: 물체가 평형 위치를 중심으로 일정한 주기와 진폭을 가지며 왕복 운동을 반복하는 현상.
• 조건: 복원력이 변위에 비례하며, 항상 평형 위치로 향해야 합니다.

F=−kx
• F: 복원력(Newton).
• k : 용수철 상수(N/m).
• x : 변위(m).
2. 용수철 진자의 원리
2.1 후크의 법칙
• 용수철은 늘어나거나 줄어든 거리(변위)에 비례하여 복원력이 작용합니다.
F=−kx
2.2 에너지 전환
• 위치 에너지: 용수철이 압축되거나 늘어났을 때 저장됩니다.
U=12kx2
• 운동 에너지: 평형 위치에서 가장 큽니다.
K=12mv2
• 단진동에서는 위치 에너지와 운동 에너지가 서로 전환되며 총 에너지는 일정합니다.
3. 가속도와 변위의 관계
3.1 가속도의 정의
• 가속도는 뉴턴의 제2법칙에 의해 복원력으로 계산됩니다.
F=ma
따라서,
a=−kmx
• a : 가속도(m/s²).
• m : 질량(kg).
3.2 가속도와 변위의 관계
• 가속도는 변위에 비례하며, 방향은 항상 평형 위치를 향합니다.
• 최대 변위( x = \pm A )에서 가속도는 최대이고, 평형 위치( x = 0 )에서는 0입니다.
a \propto -x
4. 주기와 진동수
4.1 주기 (T)
• 한 번의 진동에 걸리는 시간.
T = 2\pi \sqrt{\frac{m}{k}}
4.2 진동수 (f)
• 단위 시간당 진동 횟수.
f = \frac{1}{T}
5. 용수철 진자의 실생활 응용
1. 자동차 서스펜션 시스템
| 원리 |
| • 자동차의 서스펜션은 용수철과 댐퍼(감쇠기)로 구성되어 충격을 흡수하고 진동을 줄입니다. • 단진동의 원리를 적용해 도로의 충격으로 인한 변위를 복원력으로 억제합니다. |
| 구체적인 사례 |
| 1. 승차감 개선 • 도로의 요철이나 충격이 차량 내부에 전달되지 않도록 서스펜션이 진동을 흡수. • 용수철이 충격에 의해 압축되었다가 복원되어 차량이 안정적으로 이동. 2. 차량 안정성 유지 • 서스펜션이 바퀴의 접지력을 유지해 급회전 시 차량이 전복되지 않도록 방지. |
2. 시계 제작
| 원리 |
| • 시계의 진자나 태엽은 단진동을 통해 일정한 주기로 운동하며 시간을 측정합니다. • 용수철의 복원력을 이용해 정확한 주기를 유지합니다. |
| 구체적인 사례 |
| 1. 기계식 시계 • 태엽에 의해 용수철이 일정한 주기로 진동하며 초침을 움직입니다. • 진동수가 일정하기 때문에 시간이 정확하게 유지됩니다. 2. 진자 시계 • 중력과 복원력을 이용한 진자 운동으로 시계의 움직임을 제어합니다. |
3. 건축 설계와 지진 공학
| 원리 |
| • 고층 건물이나 다리는 단진동 모델을 이용해 진동에 대한 구조적 안정성을 분석합니다. • 용수철 모델로 건물의 자연 진동수를 계산해 지진이나 바람에 의한 흔들림을 최소화합니다. |
| 구체적인 사례 |
| 1. 지진 대응 설계 • 건물에 댐퍼와 스프링 시스템을 설치해 지진 충격을 흡수. • 예: 일본의 초고층 빌딩은 진동 저감 장치(Tuned Mass Damper, TMD)를 사용. 2. 다리 설계 • 다리의 구조적 안정성을 위해 바람이나 차량의 하중으로 인한 진동을 분석. |
4. 진동 제어 시스템
| 원리 |
| • 기계 장비나 공장에서 발생하는 진동을 용수철과 댐퍼를 통해 제어합니다. • 단진동의 주기를 조절하여 기계의 효율성과 안정성을 유지합니다. |
| 구체적인 사례 |
| 1. 산업용 기계 • CNC 기계와 같은 고정밀 장비에서 진동을 줄이기 위해 스프링 시스템을 설치. 2. 가전제품 • 세탁기의 드럼 진동을 줄이기 위해 내부에 스프링과 댐퍼를 사용. |
5. 운동 기구와 스포츠 장비
| 원리 |
| • 트램폴린과 같은 운동 기구는 용수철의 복원력을 활용해 단진동을 유도합니다. • 운동 중 발생하는 충격을 용수철로 흡수하고 되돌려주는 방식으로 설계됩니다. |
| 구체적인 사례 |
| 1. 트램폴린 • 사용자가 점프할 때 용수철이 압축되었다가 복원되며 지속적인 운동을 가능하게 합니다. 2. 테니스 라켓 • 라켓에 충격 흡수 시스템이 설치되어 진동을 줄이고 정확도를 향상시킵니다. |
6. 음향과 음악
| 원리 |
| • 피아노와 기타는 용수철과 같은 탄성을 가진 줄이 진동하며 소리를 생성합니다. • 단진동의 주파수에 따라 음의 높낮이가 결정됩니다. |
| 구체적인 사례 |
| 1. 피아노 • 피아노 줄이 망치에 의해 진동하며 일정한 주파수의 소리를 냅니다. 2. 기타 • 기타 줄이 진동하며 다양한 주파수의 음을 생성합니다. |
7. 의학에서의 응용
| 원리 |
| • 단진동 원리를 활용한 장비가 의학 분야에서 정확한 진단과 치료에 사용됩니다. |
| 구체적인 사례 |
| 1. 심장 초음파 장비 • 심장의 움직임을 단진동 모델로 분석하여 기능을 평가. 2. 리듬 분석 • 뇌파와 심장 박동의 주기를 측정하여 건강 상태를 진단. |
6. 가속도와 변위의 그래프
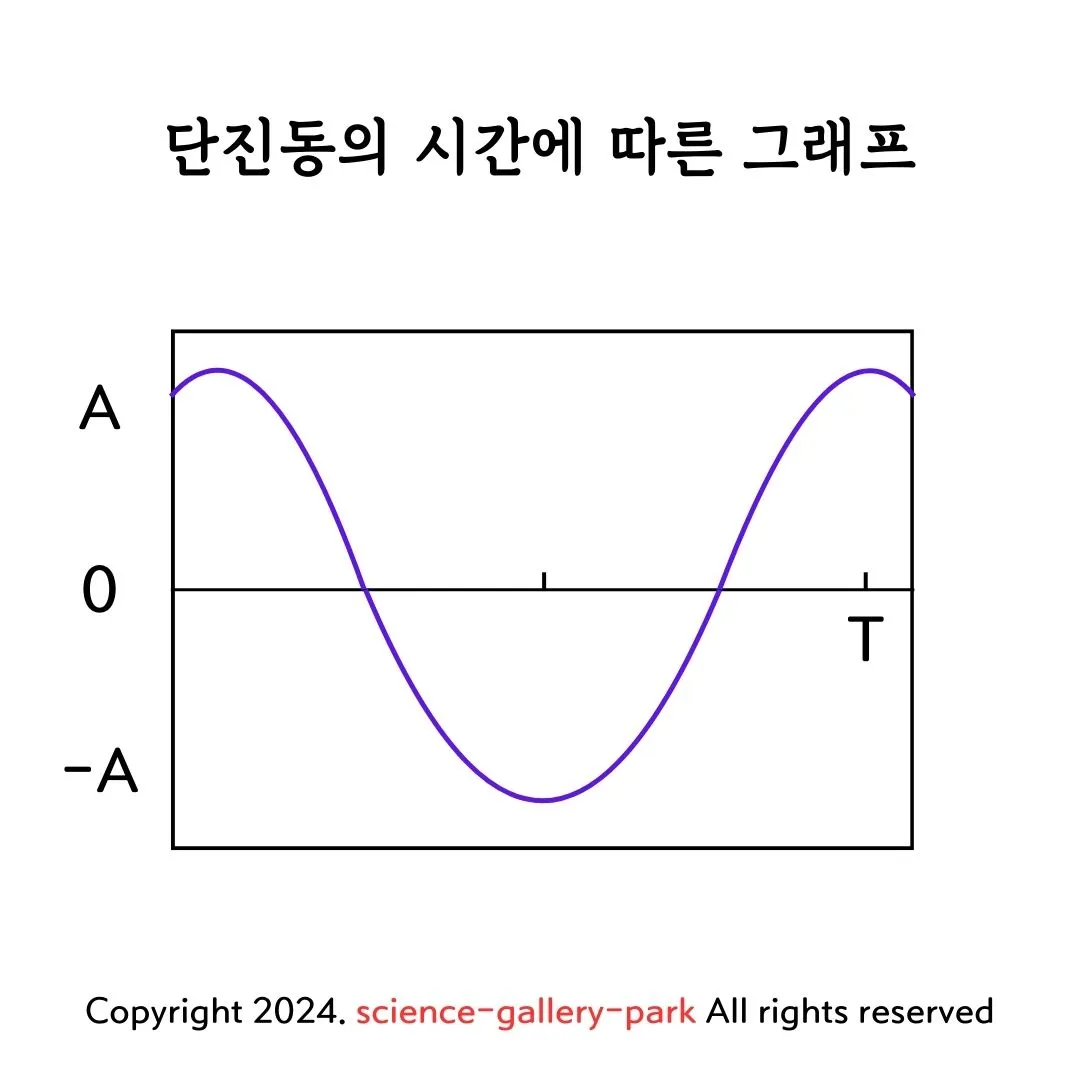
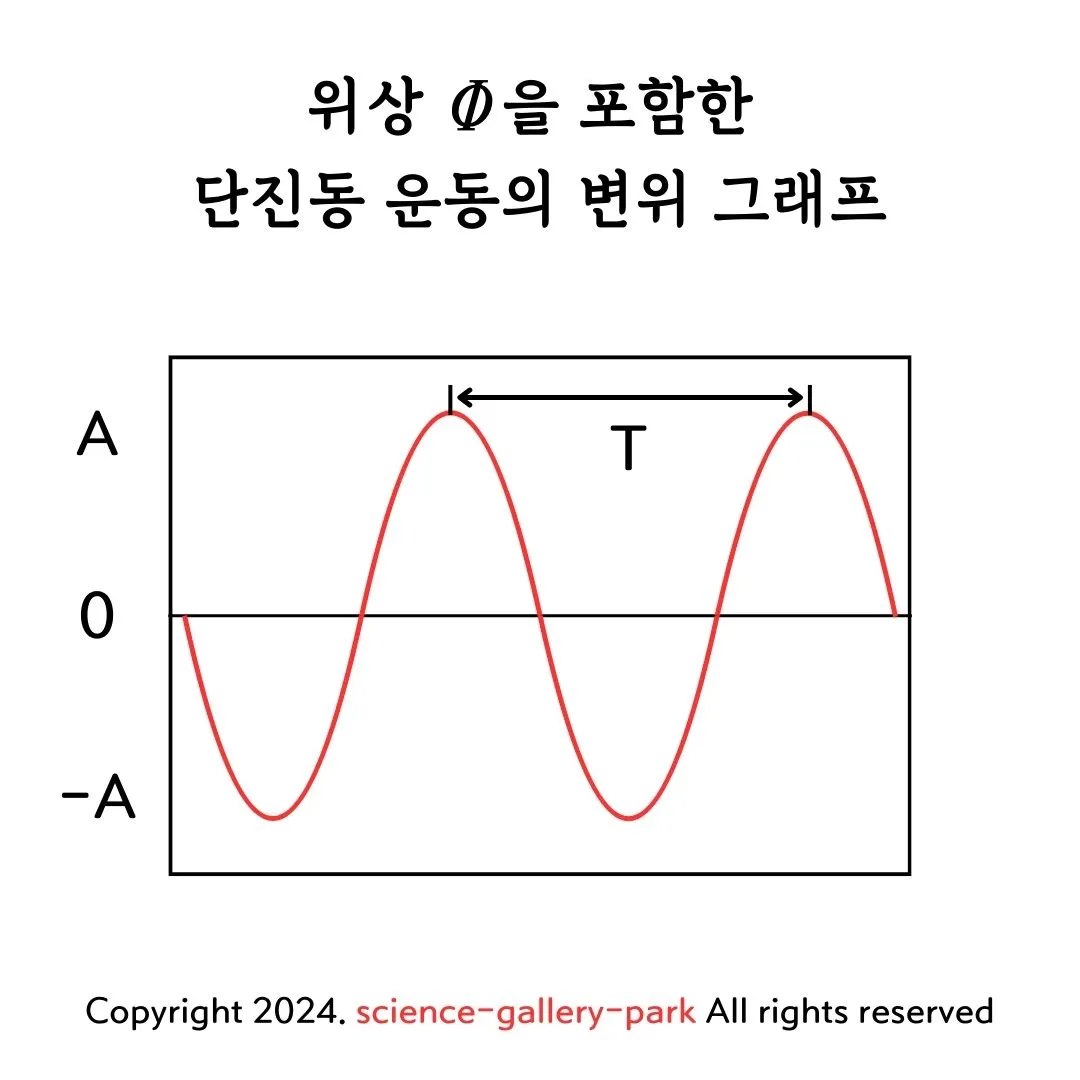
• 사인파 형태:
• 변위( x(t) )는 사인 함수로 표현됩니다.
x(t) = A\cos(\omega t)
• 가속도( a(t) )는 변위의 미분에서 얻어지는 -사인 함수로 표현됩니다.
a(t) = -\omega^2 A\cos(\omega t)
• \omega: 각진동수 ( \omega = \sqrt{k/m} ).
자주 묻는 질문 (FAQs)
1. 단진동에서 가속도와 변위의 관계는 무엇인가요?
가속도는 변위에 비례하지만, 항상 반대 방향으로 작용합니다.
2. 용수철 진자의 주기는 무엇에 의해 결정되나요?
주기는 질량( m )과 용수철 상수( k )에 의해 결정됩니다.
3. 가속도가 0일 때 변위는 어디에 있나요?
가속도가 0일 때, 변위는 평형 위치에 있습니다( x = 0 ).
4. 용수철 진자가 에너지를 잃지 않으려면 어떻게 해야 하나요?
저항(공기 저항, 마찰)이 없는 진공 상태에서만 에너지를 잃지 않습니다.
5. 단진동은 어디에서 응용되나요?
자동차 서스펜션, 지진 공학, 시계 제작 등 다양한 분야에서 사용됩니다.






