앙페르의 법칙을 통해 전류와 자기장의 상호작용을 이해하고, 다양한 문제 풀이로 실력을 늘려봅시다.
앙페르의 법칙 문제풀이

문제 1: 긴 직선 도선 주위의 자기장 계산
| 문제 |
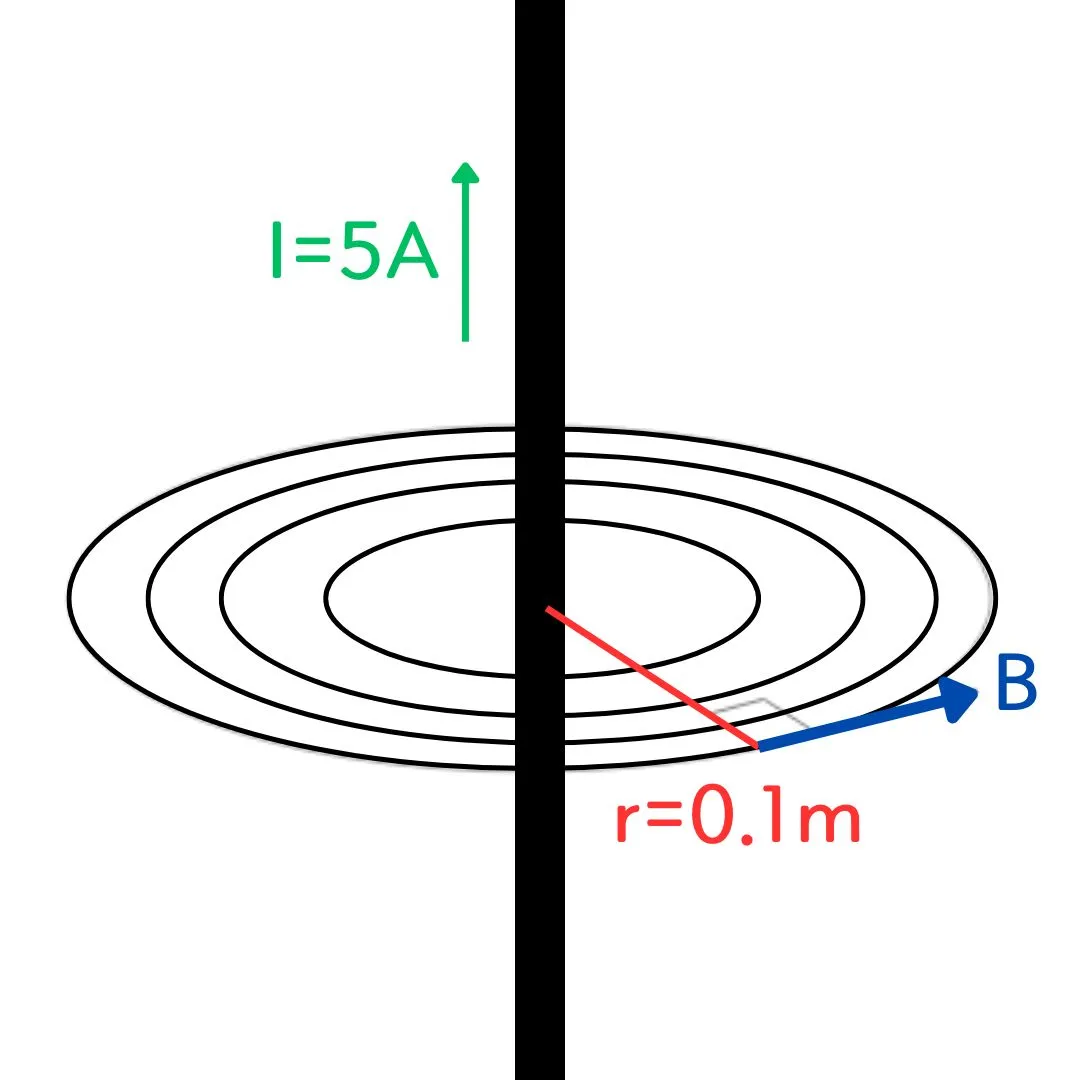
| 길이가 충분히 긴 직선 도선에 전류 $I = 5 \, \text{A}$가 흐르고 있습니다. 도선에서 반지름 $r = 0.1 \, \text{m}$ 떨어진 점에서 자기장$B$의 크기를 구하시오 |
| 풀이 |
| 1. 앙페르의 법칙 적용 앙페르의 법칙은 다음과 같이 주어집니다. $\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}}$ 여기서, • $\oint \vec{B} \cdot d\vec{l}$: 자기장이 닫힌 경로를 따라 순환하는 크기 • $\mu_0$: 진공의 투자율 ($4\pi \times 10^{-7} \, \text{N/A}^2$) • $I_{\text{enc}}$: 경로 내부의 전류 |
| 2. 대칭성 고려 긴 직선 도선 주위에서는 자기장이 원형 경로를 따라 균일합니다. 따라서 자기장의 크기 $B$는 일정하며, 원형 경로의 길이는 $2\pi r$로 나타납니다. 이를 앙페르의 법칙에 대입하면: $B \cdot (2\pi r) = \mu_0 I$ |
| 3. 자기장의 크기 계산 위 식을 $B$에 대해 풀면 $B = \frac{\mu_0 I}{2\pi r}$ 이제 값을 대입합니다. $B = \frac{(4\pi \times 10^{-7}) \cdot 5}{2\pi \cdot 0.1}$ 계산을 정리하면 $B = \frac{2 \times 10^{-6}}{0.2} = 10^{-5} \, \text{T}$ |
| 4. 결론 도선에서 $0.1 \, \text{m}$ 떨어진 점에서 자기장의 크기는 $10^{-5} \, \text{T}$입니다. |
반응형
문제 2: 솔레노이드 내부의 자기장 계산
| 문제 |
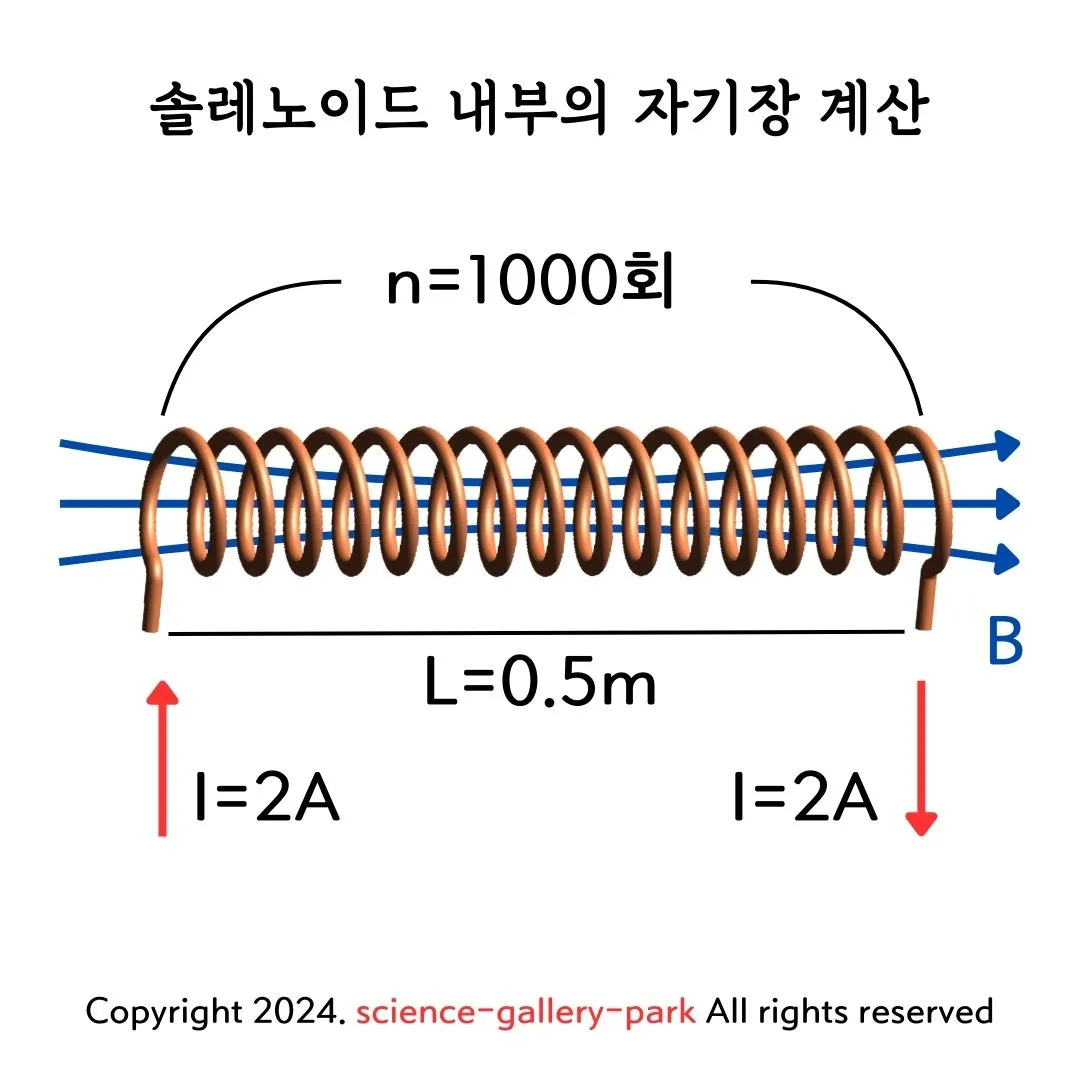
| 길이가 $L = 0.5 \, \text{m}$이고 1000회 감긴 솔레노이드에 전류 $I = 2 \, \text{A}$가 흐를 때, 솔레노이드 내부의 자기장을 구하시오. |
| 풀이 |
| 1. 솔레노이드 내부 자기장의 식 솔레노이드 내부의 자기장은 다음 식으로 표현됩니다: $B = \mu_0 n I$ 여기서, • $n$: 단위 길이당 코일 수 ($n = \frac{\text{전체 감은 횟수}}{\text{솔레노이드 길이}}$) • $I$: 솔레노이드에 흐르는 전류 |
| 2. 단위 길이당 코일 수 계산 전체 감은 횟수는 1000회, 솔레노이드의 길이는 $0.5 \, \text{m}$이므로: $n = \frac{1000}{0.5} = 2000 \, \text{turns/m}$ |
| 3. 값 대입 및 계산 자기장의 크기는 다음과 같이 계산됩니다: $B = (4\pi \times 10^{-7}) \cdot 2000 \cdot 2$ 계산을 단계별로 정리하면: $B = 8\pi \times 10^{-4} \, \text{T}$ $B \approx 5.03 \times 10^{-3} \, \text{T}$ |
| 4. 결론 솔레노이드 내부의 자기장은 약 $5.03 \times 10^{-3} \, \text{T}$입니다. |
반응형
문제 3: 원형 루프의 중심에서의 자기장 계산
| 문제 |
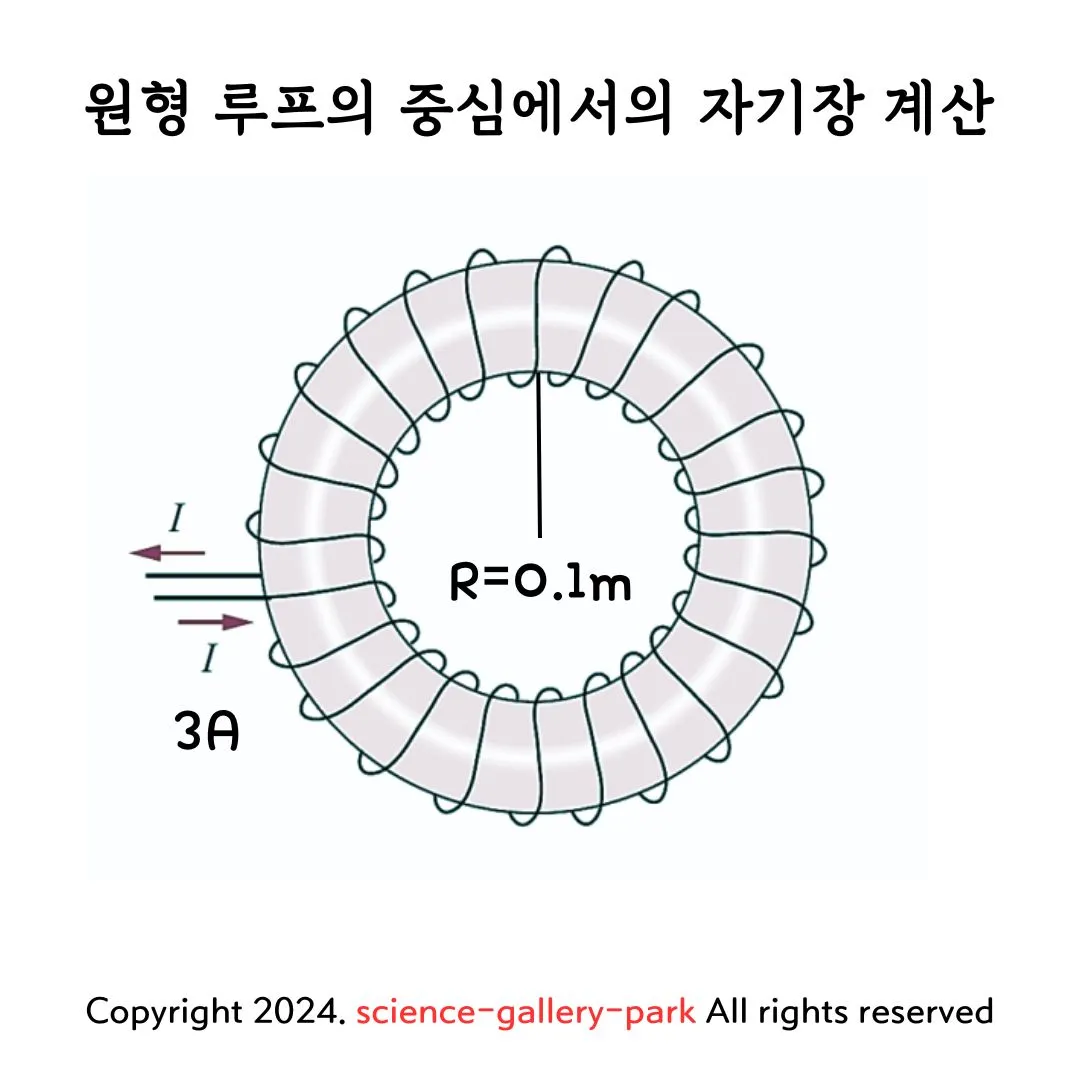
| 반지름 $R = 0.1 \, \text{m}$인 원형 도선에 전류 $I = 3 \, \text{A}$가 흐르고 있습니다. 원형 루프의 중심에서 자기장의 크기를 구하시오. |
| 풀이 |
| 1. 원형 루프의 중심 자기장 식 원형 루프 중심에서의 자기장은 다음 식으로 표현됩니다.  $B = \frac{\mu_0 I}{2R}$ 여기서, • $R$: 원형 루프의 반지름 • $I$: 원형 루프를 통과하는 전류 |
| 2. 값 대입 및 계산 식에 주어진 값을 대입합니다. $B = \frac{(4\pi \times 10^{-7}) \cdot 3}{2 \cdot 0.1}$  계산을 정리하면: $B = \frac{12\pi \times 10^{-7}}{0.2}$ $B = 1.88 \times 10^{-6} \, \text{T}$ |
| 3. 결론 원형 도선 중심에서의 자기장은 약 $1.88 \times 10^{-6} \, \text{T}$입니다. |
반응형
정리된 풀이를 통한 학습 포인트
1. 문제 1에서는 긴 직선 도선 주위에서 대칭성을 활용하여 자기장을 계산했습니다.
2. 문제 2에서는 솔레노이드의 구조와 내부 자기장의 균일성을 이해했습니다.
3. 문제 3에서는 원형 도선 중심에서의 자기장을 계산하며 전류와 반지름의 상관관계를 확인했습니다.
이 세 가지 문제는 앙페르의 법칙이 전류와 자기장 사이의 관계를 구체적으로 어떻게 나타내는지 잘 보여줍니다.






 }
}