상수함수(Constant Function)는 변수의 값과 상관없이 항상 일정한 출력값을 가지는 함수입니다. 이 함수는 그래프 상에서 평행선의 형태로 나타나며, 수학의 기초 개념을 배우는 데 중요한 역할을 합니다. 이번 포스팅에서는 상수함수의 정의, 특성, 그래프, 실생활에서의 활용을 알아보겠습니다.
상수함수

1. 상수함수의 정의
상수함수는 입력 변수의 값과 상관없이 일정한 출력을 제공하는 함수로, 일반적으로 다음과 같이 표현됩니다.
f(x) = c
여기서,
• c : 상수 값으로, 모든 x 값에 대해 항상 동일한 출력 값을 나타냅니다.
예를 들어, 함수 f(x) = 5 는 상수함수로, x 값이 무엇이든 항상 결과가 5입니다.
2. 상수함수의 특성
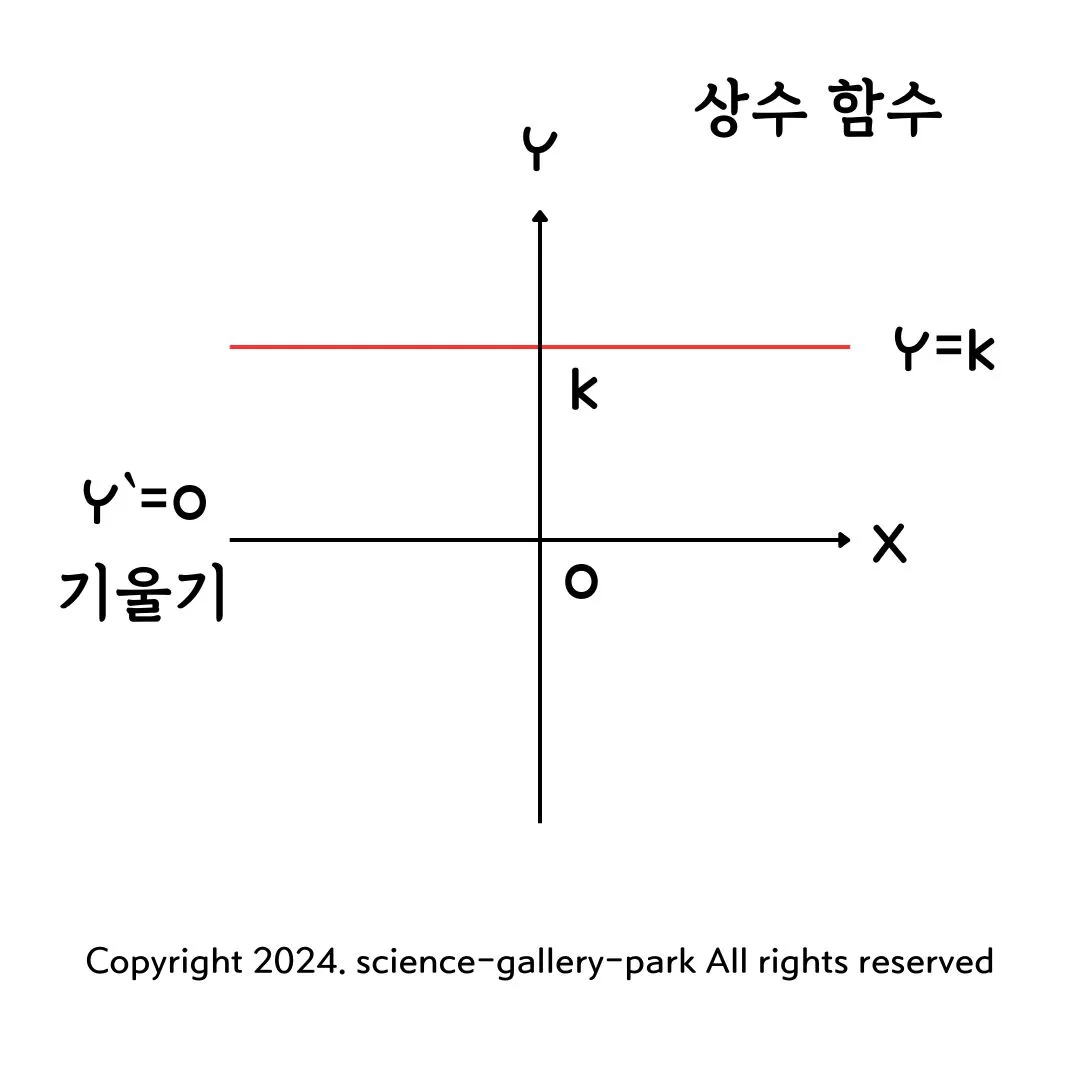
1. 변화가 없음
• 상수함수는 변수 x 가 변해도 출력 값이 변하지 않고 일정하게 유지됩니다. 이는 그래프 상에서 수평선으로 나타나게 됩니다.
2. 기울기가 0
• 상수함수의 그래프는 수평선 형태이기 때문에 기울기가 0입니다. 이는 다음과 같이 나타낼 수 있습니다.
$f{\prime}(x) = 0$
상수함수의 모든 지점에서 변화율이 0임을 의미합니다.
3. 함수의 형태
• 모든 상수함수의 형태는 f(x) = c 로, 이때 c 는 변하지 않는 고정된 값입니다.
3. 상수함수의 그래프
상수함수의 그래프는 수평선을 나타내며, y축의 y = c 값에서 수평으로 그려집니다. 예를 들어, f(x) = 3 이라면 이 함수의 그래프는 y축의 y = 3 에서 수평선을 이루며, x축에 평행하게 그려집니다.
그래프 예시
1. f(x) = 4 인 상수함수의 그래프는 y = 4 에서 수평선을 그리게 됩니다.
2. f(x) = -2 라면, 이 함수의 그래프는 y = -2 에서 수평선을 그립니다.
4. 상수함수의 실생활 활용 예제
1. 고정된 가격 계산
• 상수함수는 고정된 가격이나 일정한 비용 계산에서 활용될 수 있습니다. 예를 들어, 한달에 50달러의 고정 요금을 내는 서비스의 비용은 항상 50달러로 표현됩니다.
2. 온도 조절 장치
• 특정 온도로 설정된 온도 조절 장치는 실내 온도를 일정하게 유지하므로, 상수함수의 개념과 유사하게 작동합니다.
3. 정해진 속도 유지
• 자율주행 차량이 일정한 속도를 유지하도록 설정되어 있다면, 주행 속도를 일정하게 유지하는 속도 또한 상수함수로 표현될 수 있습니다.
5. 상수함수를 공부하기 위한 팁
1. 변화 없는 값을 그래프로 시각화하기
• 상수함수는 그래프에서 항상 수평선을 이루므로, x 값이 변해도 출력 값이 변하지 않는 것을 시각적으로 이해해 보세요.
2. 기울기가 0인 개념 익히기
• 상수함수의 변화율이 0이라는 개념을 익히고, 변화가 없음을 수학적으로 이해해 보세요.
3. 다양한 예제를 통해 상수함수의 활용 확인
• 실생활에서 일정한 고정값을 가지는 상황을 찾고, 이를 상수함수로 표현해 보면서 개념을 확립해 보세요.
6. 상수함수와 관련된 공식 요약
• 함수의 형태: f(x) = c
• 기울기: $f{\prime}(x) = 0$
결론
상수함수(Constant Function)는 수학에서 일정한 값을 유지하는 기본적인 함수 형태로, 기울기 0의 수평선 형태로 나타납니다. 상수함수의 개념을 이해하면, 일정한 출력을 가지는 시스템을 수학적으로 분석하고 실생활 문제에 적용할 수 있습니다. 상수함수는 기초적인 개념이지만, 다양한 문제를 해결하는 데 유용한 역할을 합니다.






 }
}