삼각비(Trigonometric Ratios)는 직각삼각형에서 각도와 변의 길이 사이의 비율을 의미하며, 사인(sin), 코사인(cos), 탄젠트(tan) 등의 용어로 나타냅니다. 삼각비는 기하학, 물리학, 공학 등에서 길이와 각도 관계를 계산하는 데 필수적인 도구로 사용됩니다. 이번 포스팅에서는 삼각비의 정의, 공식, 삼각비의 성질, 실생활 활용을 중심으로 알아보겠습니다.
삼각비

1. 삼각비의 정의
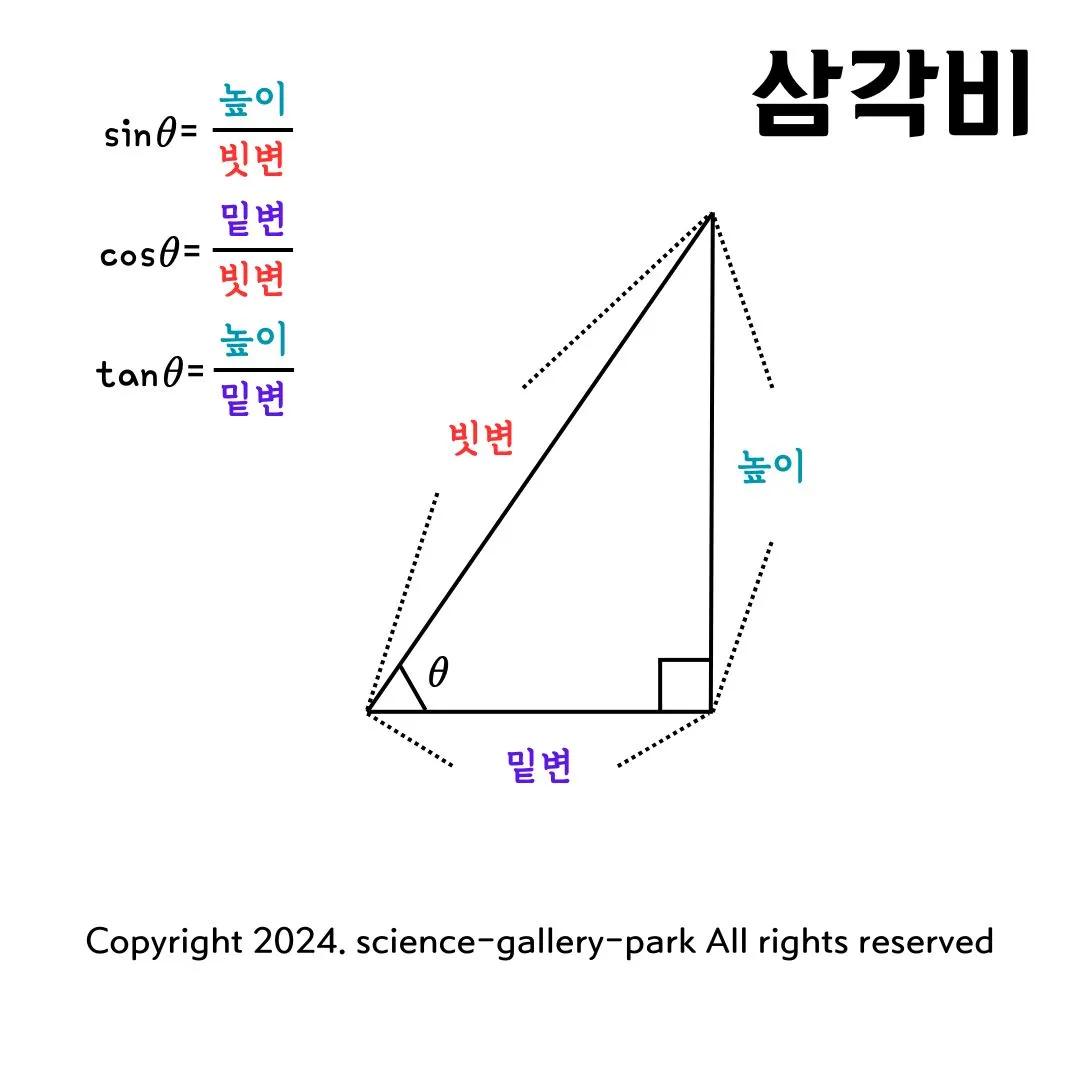
삼각비는 직각삼각형에서 한 각에 대한 변의 길이 비율을 나타냅니다. 삼각비는 사인(sin), 코사인(cos), 탄젠트(tan)으로 나뉘며, 각 삼각비는 다음과 같은 관계로 정의됩니다.
1. 사인(Sine): 빗변에 대한 높이의 비율
$\sin \theta = \frac{\text{높이}}{\text{빗변}}$
2. 코사인(Cosine): 빗변에 대한 밑변의 비율
$\cos \theta = \frac{\text{밑변}}{\text{빗변}}$
3. 탄젠트(Tangent): 밑변에 대한 높이의 비율
$\tan \theta = \frac{\text{높이}}{\text{밑변}}$
예를 들어, 각 $\theta$가 주어졌을 때, 직각삼각형에서 변의 길이를 이용해 사인, 코사인, 탄젠트 값을 구할 수 있습니다.
2. 삼각비의 성질과 특징
1. 기본 삼각비 관계식
• 삼각비는 서로 관계를 가지며, 다음과 같은 기본적인 삼각비 관계식이 성립합니다.
$\tan \theta = \frac{\sin \theta}{\cos \theta}$
2. 피타고라스 정리와의 관계
• 삼각비는 피타고라스 정리를 기반으로 계산할 수 있습니다.
• 예를 들어, 빗변의 제곱은 높이와 밑변의 제곱의 합과 같다는 피타고라스 정리를 이용하여 삼각비를 구할 수 있습니다.
3. 각도의 변화에 따른 삼각비 변화
• 각도가 커지면 사인과 탄젠트 값은 증가하고, 코사인은 감소합니다. 0도에서 90도까지 각도가 변할 때 삼각비 값도 달라집니다.
4. 삼각비 표
• 0도, 30도, 45도, 60도, 90도의 삼각비 값은 다음과 같습니다.
| θ | $\sin \theta $ | $\cos \theta $ | $ \tan \theta $ |
| 0° | 0 | 1 | 0 |
| 30° | 0.5 | 0.866 | 0.577 |
| 45° | 0.707 | 0.707 | 1 |
| 60° | 0.866 | 0.5 | 1.732 |
| 90° | 1 | 0 | undefined |
3. 삼각비의 활용법
삼각비는 다양한 문제에서 길이와 각도의 관계를 구하는 데 활용됩니다. 직각삼각형의 변의 길이를 구하거나, 높이와 거리를 계산하는 데 유용하게 쓰입니다.
1. 변의 길이 계산
• 주어진 각도와 한 변의 길이를 이용해 나머지 변의 길이를 구할 수 있습니다.
• 예제: 30도의 각도와 빗변이 10인 삼각형에서 높이 $(\sin 30° = \frac{1}{2})$는 $10 \times \sin 30° = 5$입니다.
2. 거리와 각도 계산
• 삼각비를 사용하여 높은 건물의 높이 또는 건물에서 일정 거리만큼 떨어진 지점에서 측정된 각도를 활용하여 높이를 계산할 수 있습니다.
• 예제: 길거리에서 나무 꼭대기까지의 각도가 45도이고, 나무에서 10m 떨어져 있다면 나무 높이는 $10 \times \tan 45° = 10m$입니다.
4. 삼각비의 실생활 활용 예제
1. 건축과 설계
• 건축물의 각도와 높이를 정확히 측정하기 위해 삼각비를 사용합니다. 예: 건물 높이 계산, 사다리의 길이 계산 등
2. 항공 및 항법
• 비행기나 선박의 항로를 계산할 때, 삼각비를 이용하여 각도와 거리를 정확히 조정합니다.
3. 물리학
• 삼각비는 힘의 분해, 가속도 분석 등 물리학 문제에서 벡터와 각도를 계산하는 데 사용됩니다.
4. 측량과 지형 분석
• 지형의 높이와 거리를 분석할 때, 삼각비를 통해 산의 높이나 거리 측정에 사용됩니다.
5. 삼각비를 공부하기 위한 팁
1. 삼각비 표 외우기
• 30도, 45도, 60도 등 기본 각도에 대한 삼각비 값을 외워두면 문제 해결에 도움이 됩니다.
2. 삼각비 공식 연습하기
• 사인, 코사인, 탄젠트 관계를 숙지하고 다양한 문제를 풀며 삼각비 공식을 연습하세요.
3. 실생활에서의 삼각비 적용하기
• 건물 높이, 각도 측정 등 주변에서 삼각비를 어떻게 적용할 수 있을지 생각해 보세요.
6. 삼각비의 기본 공식 요약
1. 사인: $\sin \theta = \frac{\text{높이}}{\text{빗변}}$
2. 코사인: $\cos \theta = \frac{\text{밑변}}{\text{빗변}}$
3. 탄젠트: $\tan \theta = \frac{\text{높이}}{\text{밑변}}$
4. 기본 삼각비 관계식: $\tan \theta = \frac{\sin \theta}{\cos \theta}$
결론
삼각비(Trigonometric Ratios)는 직각삼각형에서 각도와 변의 관계를 계산하는 중요한 도구로, 기하학, 물리학, 건축 등에서 필수적으로 사용됩니다. 삼각비를 이해하고 활용하면 길이와 각도 계산을 쉽게 수행할 수 있으며, 실생활에서도 다양한 문제 해결에 적용할 수 있습니다.






 }
}